Por exemplo:
Num pátio existem automóveis e bicicletas. O número total de rodas é 130 e o número de bicicletas é o triplo do número de automóveis. Determine:
a) O número de automóveis que se encontram no pátio;
b) O número de bicicletas que se encontram no pátio;
c) O número de veículos que se encontram no pátio.
SOLUÇÃO:
Inicialmente, teremos que equacionar o problema, veja:
x = número de automóveis e
y = número de bicicletas
O número total de rodas é igual a 130, ou seja, 4x + 2y = 130. Pois cada automóvel contém 4 rodas (4 vezes o número de automóveis, 4x) e cada bicicleta contém 2 rodas (2 vezes o número de bicicletas, 2y).
O número de bicicletas é o triplo do número de automóveis, ou seja, y = 3x.
Daí, as duas equações: 4x + 2y = 130 e y = 3x formam um sistema de duas equações do 1º grau com duas incógnitas.
Representamos da seguinte maneira:
Existem vários pares ordenados que satisfazem cada uma das equações:
Mas apenas um par ordenado (13,39) é solução do sistema, ou seja, é solução das duas equações ao mesmo tempo.
Portanto, x = 13 e y = 39, S = {(13,39)}.
Nem sempre resolver um sistema por tentativas é mais fácil. Por isso, resolveremos o sistema pelo método algébrico: o método da substituição.
MÉTODO DA SUBSTITUIÇÃO
Como y já está isolado no 1º membro na equação (II) , apenas substituímos y por 3x na equação (I).
Veja:
(I) 4x + 2(3x) = 130 => 4x + 6x = 130 => 10x = 130
Dividindo ambos os membros da equação por 10, temos:
Da equação (II), ou seja, y = 3x, temos que: y = 3. 13 => y = 39.
Então:
x = 13 = número de automóveis
y = 39 = número de bicicletas
a) O número de automóveis que se encontram no pátio;
13 automóveis
b) O número de bicicletas que se encontram no pátio;
39 bicicletas
c) O número de veículos que se encontram no pátio.
x + y = número de veículos
O número de veículos é: 13 + 39 = 52
Vejam outros problemas envolvendo sistemas de equações do 1º grau com duas incógnitas.
Clique em cada lista abaixo:
Resolvam, por comentários, os problemas abaixo:
1) Numa lanchonete, 2 copos de refrigerantes e 3 coxinhas custam R$ 5,70. O preço de 3 copos de refrigerantes e 5 coxinhas é R$ 9,30. Quais os preços de cada coxinha e cada copo de refrigerante?
2)Um marceneiro recebeu 74 tábuas de compensado. Algumas com 6 mm de espessura e outras com 8 mm de espessura. Quando foram empilhadas, atingiram a altura de 50 cm. Quantas tábuas de 8mm ele recebeu?
OBS: Das listas mencionadas acima, escolha pelo menos um problema para apresentar a turma na próxima aula.
Clique em comentários, logo abaixo
.
.
.
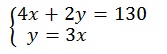



Eu posso dizer que
ResponderExcluir1 copo de refrigerante custa x reais e
1 coxinha custa y reais?
e depois eu faço o que?
vc coloca x+y=2
Excluirx-y=2
agora e so resolver
ExcluirComo são dois copos de refrigerantes, você pode representar por 2x, três coxinhas por 3y, três copos de refrigerantes por 3x e cinco coxinhas por 5y...
ResponderExcluirleia um pouco mais e veja o que foi dado no problema que lhe permite equacioná-lo.
Att. Ilton
Professor Consegui fazer as questões.
ResponderExcluir1° {2x+3y=5,70
{3x+5y=9,30 isolando Y => 3x+5y=9,30
5y=9,30-3x
y=9,30-3x/5
2x+3y=5,70
2x+3(9,30-3x/5)=5,70 ai tira mmc, que da 5
10x+3(9,30-3x)=28,5
10x+27,9 -9x=28,5
10x-9x=28,5-27,9
x=0,6
Y=9,30-3x/5
Y=9,30-3.0,6/5
Y=9,30-1,8/5
Y=7,5/5
Y=1,5 O valor da coxinha é 0,6 e o do
refrigerante 1,5 (0,6;1,5)
2°questão
{x+y=74
{6x+8y=500 esses 500 transformei de 50cm para 500mm, ja que as tabúas estão em mm.
{x+y=74 .(-6)
{6x+8y=500
{-6x-6y=-444
{6x+8y=500
____________
2y=-56 x+y=74
y=-56/2 x+28=74
y=-28 x=74-28
x=46
Portanto são 46 Tabuas de 6mm e 28 tabuas de 8mm . (46;28).
Kelvin Goldberg 9°A Manhã
Muito bem Kelvin... ponto garantido!
ExcluirAtt. Ilton Bruno
Ilton, não vou escrever o cáuculo, pois quase não dar pra entender, um em cima do outro, mas a resposta deu o mesmo resultado do de kelvin, tudo certo, ele mim ajudou: 1° Questão: X igual à :0,60 centavos, e Y igual à: 1,50 centavos. 2° questão: 6mm igual à 46 tabuas e 8mm igual à 28 tabuas. ASS: Kaline araújo, 9° ano A
ResponderExcluir1º questão 2copos de refi+3 coxinha=5,70 2x+3y=5,70 3 copos de refri+5 coxinhas=9,30 3x+5y=9,30 2x+3y=5,70 2x+6(3x)=5,70=2x+18x=5,7020x=5,70=x=5,70 sobre 20=0,285 2x+6(3x)=20x=9,30=9,30 sobre20=0,465 3y-6(5y)=3y-30y=5,70=y=570 sobre27=0,211 3y-6(5y)=9,30 = 930 sobre 27 que é igual a 0,344= y=061
ResponderExcluirO VALOR DE X=0,75, E O DE Y=0,61
2ºQUESTÃO
74 tábuas x+y= x 6 mm x=6 e y=5=74 y 8 mm
50 CM 6x+8y=74
y=50x
6mm 46 tábuas
8mm 28 tabuas
Aluna : luana Clementino Policarpo 9 ano " A "
Obrigado pela participação e dedicação...
ResponderExcluirabraços a todos!
Att. Ilton
Este comentário foi removido pelo autor.
ResponderExcluira questão 2 da primeira lista alguém me ajuda a fazer
ResponderExcluirurgenteeeeeeeeeeeeee