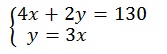2015: Bullying: Provocações sem limites

Diga não ao Bullying, denuncie... 

A intenção de compartilhar este filme com os meus alunos é, principalmente, estimular as possíveis vítimas e/ou testemunhas a denunciarem essa prática tão presente no dia-a-dia das escolas em todo o mundo. Assim como, tentar conscientizar os agressores do mal em que está praticando...

Olá pessoal, epero que tenham gostado do filme. Agora, vamos discutir mais um pouco, observem a proposta a seguir.

• Com auxílio dos netbook's educacionais (Programa UCA), poste seu comentário a respeito do tema e do filme assistido em sala.
  
  

Bullying: Provocações Sem Limites

Informações do Filme:
Título Original: Bullying
Título Traduzido: Bullying: Provocações Sem Limites
Gênero: Drama
Ano de Lançamento: 2009
Duração: 1 Hora e 29 Minutos

Sinopse: 

Jordi é um adolescente que perdeu recentemente seu pai e que, junto à sua mãe, decide mudar de cidade para começar uma nova vida. Em princípio tudo parece bem, mas o destino reservado para ele será uma terrível surpresa já que quando Jordi passar pelo portão da nova escola, cruzará sem saber a tenebrosa fronteira de um novo inferno.

Trailer

2ª Lista de Exercícios (Razão, Proporção e Teorema de Tales)

2ª Lista de Exercícios
(Razão, Proporção e Teorema de Tales)

1)      Ao analisar a planta de uma quadra de um determinado condomínio, o engenheiro constatou a ausência de algumas medidas nas divisas de certos lotes residenciais. Ele precisa calcular essas medidas do seu próprio escritório, com base nas informações da planta. Observe o desenho detalhado da situação:
Com base na planta devemos calcular os lados x e y dos lotes. Veja que as laterais dos lotes 1, 2 e 3 são perpendiculares às ruas A e B.

2)      O mapa ao lado mostra quatro estradas paralelas que são cortadas por três vias transversais. Algumas das distâncias entre os cruzamentos dessas vias e estradas estão indicadas no mapa (em km), mas as outras precisam ser calculadas. Complete o mapa com as distâncias que faltam.

3)      A figura 1 abaixo mostra os quarteirões de um bairro com suas respectivas medidas, qual o comprimento aproximado da praça?

Figura 1

4)      Um engenheiro resolveu contar em passos a distância do obelisco da cidade que visitava até o primeiro cruzamento de cada uma das quatro ruas que começavam ali. Quando terminou de percorrer a terceira, percebeu que os quarteirões formavam paralelas. Ele consegue saber quantos passos terá o último trecho com base nas medidas anotadas no mapa? Considere a figura 2.

Figura 2

5)      Resolva as seguintes proporções:

6)      A soma da idade do pai e do filho é 45 anos. A idade do pai está para a idade do filho, assim como 7 está para 2. Determine a idade do pai e do filho.

7)      Para fazer 600 pães, são gastos, em uma padaria, 100 Kg de farinha. Quantos pães podem ser feitos com 25kg de farinha?

DESAFIOS:

1º      O prefeito de uma cidade do interior do estado deseja expandir as exportações, para isso terá que construir uma ponte de um extremo a outro de um lago, como o mostrado no desenho à direita, mas primeiro precisa saber quanto mede essa extensão. Como ele pode descobrir?

2º      Em uma sala de aula, a razão de moças para o número de rapazes é de 5/4. Se o número total de alunos desta turma é de 45 pessoas, caso exista uma festa quantas moças ficariam sem par?

Resolvam e entreguem a lista de exercícios na próxima aula

Resolvam, através dos comentários:
- O exercício 3)
- 2º DESAFIO.

Baixe a lista completa (em pdf) no link abaixo, é só clicar:

2ª Lista de Exercícios (Razão, Proporção e Teorema de Tales) 9º ano - Ilton Bruno

1ª Lista de Exercícios - Razão e Proporção

RAZÃO

A palavra razão vem do latim ratio e significa a divisão ou o quociente entre dois números P e Q, denotada por:

Exemplo: A razão entre 40 e 10 é 4, pois:

  

 PROPORÇÃO

 A palavra proporção vem do latim proportione e significa uma relação entre as partes de uma grandeza, ou seja, é uma igualdade entre duas razões. 

A proporção entre

  

é a igualdade:

 

 Exemplo: Determinar o valor de X para que a razão X/24 esteja em proporção com 5/6.

Solução:

Monte e resolva a proporção:  

 

Abaixo segue uma lista de exercícios para a próxima aula e escolha pelo menos 2 para resolver através dos comentários, e consequentemente em sala de aula:

Clique...  1ª Lista de Exercícios: Razão e Proporção

Um abraço a todos e boa sorte!

Coeficientes de Equações do 2º grau

Pessoal, no link a seguir vocês terão a chance de praticar bastante sobre como identificar os coeficientes de uma equação do 2º grau, prática esta fundamental para resolver equações do 2º grau pela fórmula geral de resolução...

Clique AQUI

Fórmula geral de resolução de uma equação do 2º grau, conhecida no Brasil como Fórmula de Bhaskara

Fonte: http://www.warlisson.com.br

Atividade - Equação do 2º grau

Pessoal, segue uma lista de exercícios sobre Equações do 2º Grau. Peço que a faça, pois é praticando que vocês terão certeza das dúvidas... kkkkkk

Qualquer dúvida a gente tira em sala de aula! 

Clique aqui: Atividade - Equação do 2º grau

3ª Atividade - Equações do 2º grau incompletas

Olá a todos e todas, estou postando mais uma atividade sobre equações do 2º grau incompletas. Pois, além da atenção nas aulas, tentar resolver questões também é muito importante. Então, pratiquem e tirem suas dúvidas sempre que possível.

Para abrir ou baixar a atividade clique aqui

2ª Atividade - Equações do 2º grau Incompletas

Segue o link da atividade sobre equações do 2º grau incompletas, então pratiquem bastante para que possamos tirar as possíveis dúvidas em sala de aula ou pelos redes sociais.

Clique aqui => 2ª Atividade - Equações do 2º grau incompletas

1ª Lista de Exercícios - Equações do 2º grau Incompletas

Pessoal, vejam a resolução de Equações do 2º grau incompletas e em seguida uma lista de exercícios para auxiliá-los em vossos estudos.

Bom desempenho!!!

A forma geral de uma equação do 2º grau é escrita assim ax² + bx + c = 0, onde a, b e c são números reais com a ≠ 0. 

Quando b = 0 ou c = 0 ou b = 0 e c = 0, a equação do 2° grau é incompleta.

Veja a resolução de equações do 2° grau incompletas:

Tipo: ax²  = 0

percebemos que a ≠ 0, b = 0 e c = 0

isolando o x² no primeiro membro, temos

ax²/a = 0/a  (dividindo ambos os membros por a)

x² = 0

como a equação é do 2º grau, existem dois valores para x que satisfazem a equação, é fácil de perceber que só o x = 0 torna a igualdade verdadeira. 

Logo, as duas raízes são:

x' = x" = 0

S = {0}

Tipo: ax² + bx = 0

percebemos que a ≠ 0, b = 0 e c = 0

Colocando o x em evidência, temos:

 x(ax + b) = 0

Quando o produto de dois números reais é igual à zero, então pelo menos um dos fatores é igual a zero.

No entanto:

x = 0      ou       ax + b = 0 

então, x' = 0. 

Agora vamos encontrar o valor da outra raiz:

ax + b = 0, isolando o valor de x no primeiro membro, temos:

x" = -b/a 

S = {-b/a;0}

Tipo: ax² + c = 0

Percebemos que a ≠ 0, b = 0 e c ≠ 0

isolando o x² no primeiro membro, temos

x² =  - c/a

√x² = ± √-c/a

x = ± √-c/a

Clique em: Lista de Exercícios (Equações do 2º grau - incompletas)

Sistema de equações do 1º grau com duas incógnitas

Muitas vezes, quando tentamos resolver um problema acabamos nos deparando com duas equações de duas incógnitas...

Por exemplo:

Num pátio existem automóveis e bicicletas. O número total de rodas é 130 e o número de bicicletas é o triplo do número de automóveis. Determine: 

a) O número de automóveis que se encontram no pátio;

b) O número de bicicletas que se encontram no pátio;

c) O número de veículos que se encontram no pátio.

SOLUÇÃO:

Inicialmente, teremos que equacionar o problema, veja:

x = número de automóveis e 

y = número de bicicletas

O número total de rodas é igual a 130, ou seja, 4x + 2y = 130. Pois cada automóvel contém 4 rodas (4 vezes o número de automóveis, 4x) e cada bicicleta contém 2 rodas (2 vezes o número de bicicletas, 2y).

O número de bicicletas é o triplo do número de automóveis, ou seja, y = 3x.

Daí, as duas equações: 4x + 2y = 130 e y = 3x formam um sistema de duas equações do 1º grau com duas incógnitas.

Representamos da seguinte maneira:

Existem vários pares ordenados que satisfazem cada uma das equações:

Mas apenas um par ordenado (13,39) é solução do sistema, ou seja, é solução das duas equações ao mesmo tempo. 

Portanto, x = 13 e y = 39, S = {(13,39)}.

Nem sempre resolver um sistema por tentativas é mais fácil. Por isso, resolveremos o sistema pelo método algébrico: o método da substituição.

MÉTODO DA SUBSTITUIÇÃO

Como y já está isolado no 1º membro na equação (II) , apenas substituímos y por 3x na equação (I).

Veja:

(I) 4x + 2(3x) = 130 => 4x + 6x = 130 => 10x = 130

Dividindo ambos os membros da equação por 10, temos:

Da equação (II), ou seja, y = 3x, temos que: y = 3. 13 => y = 39.

Então:

x = 13 = número de automóveis

y = 39 = número de bicicletas

a) O número de automóveis que se encontram no pátio;

    13 automóveis

b) O número de bicicletas que se encontram no pátio;

    39 bicicletas

c) O número de veículos que se encontram no pátio.

    x + y = número de veículos

    O número de veículos é: 13 + 39 = 52

Vejam outros problemas envolvendo sistemas de equações do 1º grau com duas incógnitas.

Clique em cada lista abaixo:

1ª Lista de Problemas (Sistemas de equações do 1º grau)

2ª Lista de Problemas (Sistemas de equações do 1º grau)

Resolvam, por comentários, os problemas abaixo:

1) Numa lanchonete, 2 copos de refrigerantes e 3 coxinhas custam R$ 5,70. O preço de 3 copos de refrigerantes e 5 coxinhas é R$ 9,30. Quais os preços de cada coxinha e cada copo de refrigerante?

  
2)Um marceneiro recebeu 74 tábuas de compensado. Algumas com 6 mm de espessura e outras com 8 mm de espessura. Quando foram empilhadas, atingiram a altura de 50 cm. Quantas tábuas de 8mm ele recebeu?

OBS: Das listas mencionadas acima, escolha pelo menos um problema para apresentar a turma na próxima aula.

Clique em comentários, logo abaixo

.

.

.

Questionário sobre o uso do computador e Internet - 2015

Olá pessoal, desde já lhes desejo boas vindas neste novo ano. 

De posse dos "ukinhas", respondam o questionário disponibilizado abaixo para que eu possa conhecê-los melhor sobre o uso de algumas ferramentas tecnológicas.

Aproveitamos a ocasião para discutirmos um pouco sobre os prós e os contras de algumas ferramentas.

Para responder ao questionário clique AQUI